3次関数の最大値・最小値を求める問題です。2次関数のときと話は似ていますが、3次関数には「軸」がありません・・・!
☆この問題は、こちらの記事(定義域が変化する場合の2次関数の最大・最小)を理解してから取り組みましょう!
この問題も、視覚的に捉える練習をしましょう。
その前に、$y=x^3-7x$のグラフを描いておきましょう。
$y’=3x^2-7$より、$y’=0$のとき$\displaystyle x^2=\frac{7}{3}$
$\displaystyle \therefore x = \pm \frac{\sqrt{21}}{3}$
よって増減表とグラフは以下のとおりになります。
| $x$ | $\cdots$ | $\displaystyle – \frac{\sqrt{21}}{3}$ | $\cdots$ | $\displaystyle \frac{\sqrt{21}}{3}$ | $\cdots$ |
| $y’$ | $+$ | $0$ | $-$ | $0$ | $+$ |
| $y$ | $\nearrow$ | $\displaystyle \frac{14\sqrt{21}}{9}$ | $\searrow$ | $- \displaystyle \frac{14\sqrt{21}}{9}$ | $\nearrow$ |
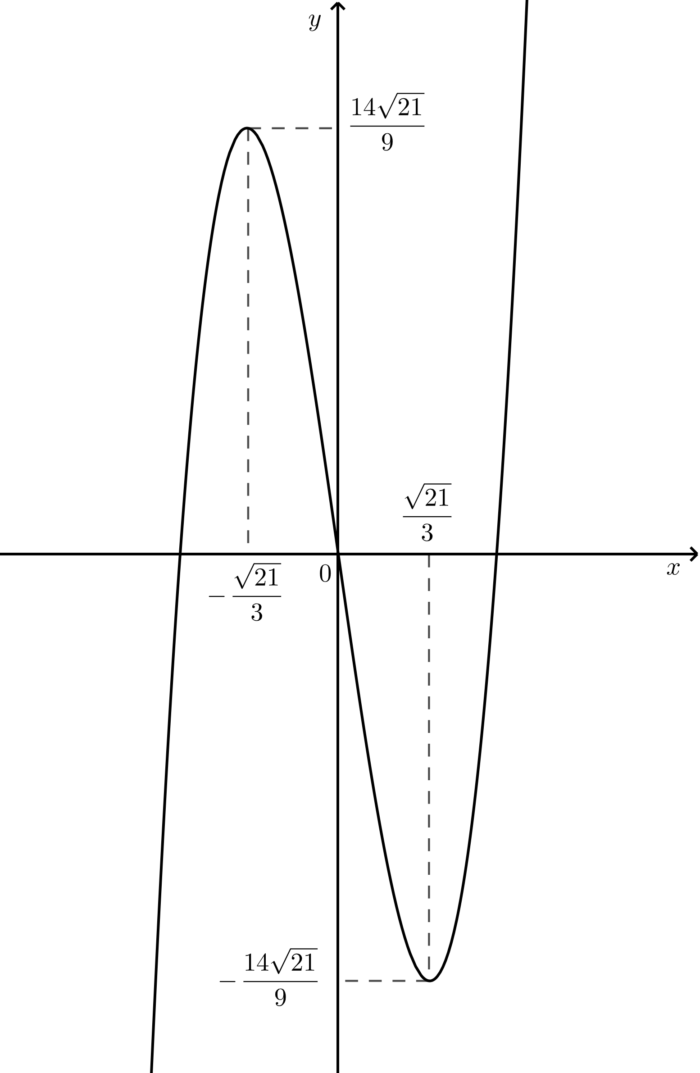
ではグラフが描けたので、定義域が $a \text{≦} x \text{≦} a + 1$ における最大・最小を考えてみましょう。下のデモ画面で、スライダーを動かすと $a$ の値が変化します。それに伴い、2本の縦線(直線 $x=a$ および直線 $x=a+1$ )も動きます。
$a$ と $a+2$ の差は $1$ で一定なので、この2本の縦線は幅が一定のまま動くことがイメージできるようにしてください。
この2本線の間は、定義域内であることが分かるよう、色を塗り、放物線が太くしてあります。
太線の部分だけ見て、$y$ はどこで最大・最小になるかを確かめてみましょう。
また、「最大値の場所を表示」「最小値の場所を表示」のラジオボタンにチェックを入れてからスライダーを動かすと、最大あるいは最小となる場所を点で示してくれます。
※極大・極小をとる $x$ の値が小数になっていますが、上図で示したとおり$\displaystyle \pm \frac{\sqrt{21}}{3}$ と読み替えてください。
aの値:
動かしてみて、$a$ がどの値の時にどこで最大・最小をとるのかイメージできましたか?
2次関数の時は軸と定義域の位置関係に着目でしたが、3次関数のときはもう少し深く考える必要があります(とはいえ、2次関数の場合とそんなに変わりません)。
最大値
「最大値の場所を表示」のラジオボタンをクリックして、$a$ の値が小さい方からスライダーを動かしてみましょう。
すると、最大の場所を表す赤丸の位置が、
(i) 定義域の右端($x=a+1$ で最大)
↓①
(ii) 極大のところ($\displaystyle x=- \frac{\sqrt{21}}{3}$ で最大)
↓②
(iii) 定義域の左端($x=a$ で最大)
↓③
(iv) 定義域の右端($x=a+1$ で最大)
のように変化していったことが分かります。
なので、あとはそれぞれの境界(①、②、③)となる $x$ の値を求めましょう。
- ①は定義域の右端が極大の位置と一致するときなので、
$\displaystyle a+1 = – \frac{\sqrt{21}}{3}$
$\displaystyle \therefore a = -1 – \frac{\sqrt{21}}{3}$
が境目です。
- ②は定義域の左端が極大の位置と一致するときなので、
$\displaystyle a = – \frac{\sqrt{21}}{3}$
が境目です。
- ③は少し難しいです。この境目は定義域の両端で $y$ の値が一致し、定義域に極小の位置を含むときです。
下線が成り立つときの $a$ の値を求めてみましょう(下図の状態)。
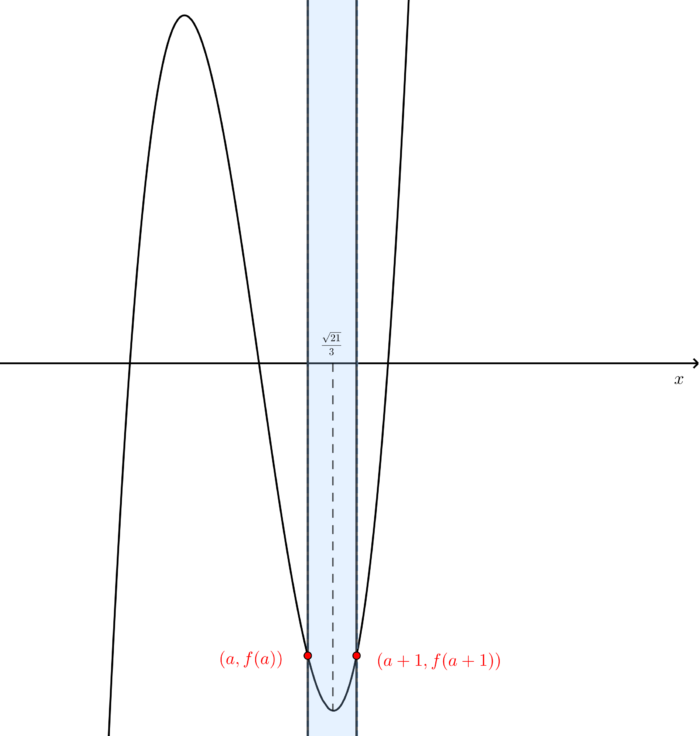
$f(x)=x^3-7x$ とおき、$f(a) = f(a+1) \cdots (*) $ を満たす $a$ を求めます。
$a^3-7a=(a+1)^3-7(a+1)$ より、
$a=-2, 1$
と求められます。
このうち、$\displaystyle a<\frac{\sqrt{21}}{3}<a+1$ を満たすのは
$a=1$
であり、これが境目です(デモ画面でもこのとき定義域の両端に青丸がついていることを確かめてください)。
最小値
「最小値の場所を表示」のラジオボタンをクリックして、スライダーを動かしてみましょう。
すると、最小の場所を表す青丸の位置が、
(i) 定義域の左端($x=a$ で最小)
↓④
(ii) 定義域の右端($x=a+1$ で最小)
↓⑤
(iii) 極小のところ($\displaystyle x= \frac{\sqrt{21}}{3}$ で最小)
↓⑥
(iv) 定義域の左端($x=a$ で最小)
のように変化していったことが分かります。
なので、最大のときと同様それぞれの境界(④、⑤、⑥)となる $x$ の値を求めましょう。
- ④の境目は、定義域の両端で $y$ の値が一致し、定義域に極大の位置を含むときです(下図の状態)。
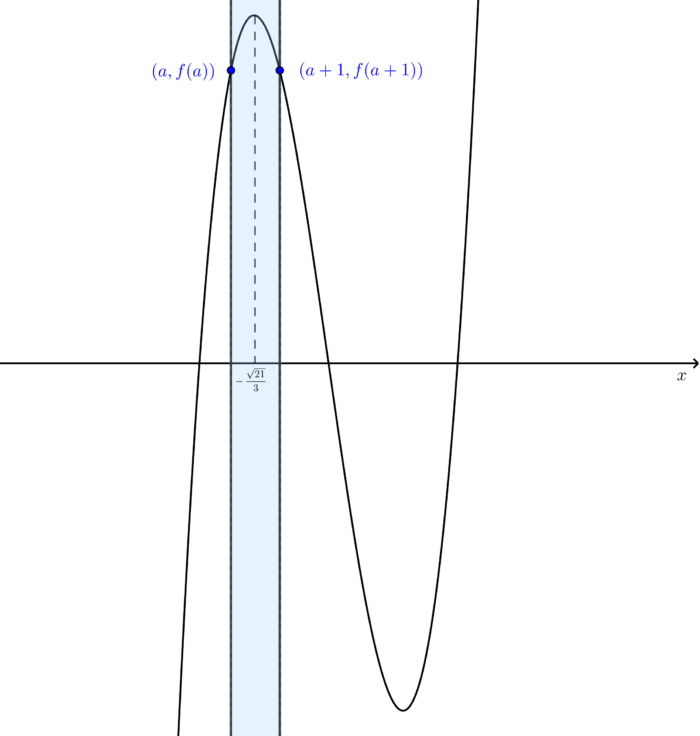
これについては、先ほどの式 $(*)$ を再び考えればよく、$a=-2, 1$ でした。
このうち、$\displaystyle a<- \frac{\sqrt{21}}{3}<a+1$ を満たすのは
$a=-2$
であり、これが境目です(デモ画面でもこのとき定義域の両端に青丸がついていることを確かめてください)。
- ⑤は定義域の右端が極小の位置と一致するときなので、
$\displaystyle a+1 = \frac{\sqrt{21}}{3}$
$\displaystyle \therefore a = -1 + \frac{\sqrt{21}}{3}$
が境目です。
- ⑥は定義域の左端が極小の位置と一致するときなので、
$\displaystyle a = \frac{\sqrt{21}}{3}$
が境目です。
まとめ
2次関数のときは軸と定義域の位置関係に着目しましたが、3次関数のときは「極大・極小と定義域の位置関係」に着目ということになるでしょう。
2次関数の場合より考え方・計算量ともにやや難しくなりますが、基本的な考え方は同じかと思います。
$a$ の値が変化すると、図形がどのように動くかイメージできるようにトレーニングを積んでください。
問題の解答
(最大値)
$\displaystyle a < -1 – \frac{\sqrt{21}}{3}, 1 \text{≦} a$ のとき $x=a+1$ で最大値 $a^3+3a^2-4a-6$
$\displaystyle -1 – \frac{\sqrt{21}}{3} \text{≦} a < – \frac{\sqrt{21}}{3}$ のとき $\displaystyle x= – \frac{\sqrt{21}}{3}$ で最大値 $\displaystyle \frac{14\sqrt{21}}{9}$
$\displaystyle – \frac{\sqrt{21}}{3} \text{≦} a < 1$ のとき $x=a$ で最大値 $a^3-7a$
※問題集によっては $a=1$ のとき $x=1, 2$ で最大値 $-6$ としているものもありますが、上記のように解答しても $a=1$ の場合だけ独立して答えてもどちらでも問題ありません。
(最小値)
$\displaystyle a<-2, \frac{\sqrt{21}}{3} \text{≦} a$ のとき $x=a$ で最小値 $a^3-7a$
$\displaystyle -2 \text{≦} a < -1 + \frac{\sqrt{21}}{3}$ のとき $x=a+1$ で最小値 $a^3+3a^2-4a-6$
$\displaystyle -1 + \frac{\sqrt{21}}{3} \text{≦} a < \frac{\sqrt{21}}{3}$ のとき $\displaystyle x= \frac{\sqrt{21}}{3}$ で最小値 $\displaystyle – \frac{14\sqrt{21}}{9}$
※問題集によっては $a=-2$ のとき $x=-2, -1$ で最小値 $6$ としているものもありますが、上記のように解答しても $a=-2$ の場合だけ独立して答えてもどちらでも問題ありません。
Comments are closed.